Many methods of causal inference try to identify a "safe" subset of variation
I have been thinking a lot about causality lately, and as a result I’ve come up with a common way to think of many different methods of causal inference that often seem to be used in science. This is probably not very novel, but I asked around whether it had a standard term, and I couldn’t find any, so I decided to write it up. I’ve personally found this model helpful, as I think it sheds light on what the limitations of these methods are, and so I thought I would write about it.
Roughly speaking, many methods of causal inference try to identify a “safe” subset of variation. That is, when trying to examine the causal effect of X on Y, they look in the variation of X to see how it relates to variation of Y. But this is possibly biased due to common causes or reverse causality (Y influencing X); so therefore to limit this problem, they find some way of partitioning X into a “safe” sort of variation that is not subject to these problems, and an “unsafe” sort that may be subject to them. Then they examine the correlation between this safe variation and Y.
The model abstracts over naive regression or multiple regression, longitudinal studies, instrumental variables, co-twin controls (Turkheimer’s “quasicausality”), and even randomized controlled trials. So to understand the common model, it is worth going through these methods of causal inference first.
Vanilla methods for causal inference
I don’t know who is going to read this blog, but I assume that most of my readers will be familiar with regression and experiments. Still it might be worth taking a recap:
Regression is the most naive method of causal inference; you’ve got two variables X and Y, and then you assume that any association between X and Y is due to a causal effect of X on Y. With regression, it is then straightforward to use data to see how much X correlates with Y and use this as the causal estimate. This is invalid if Y affects X, or if there is some common factor Z which affects both X and Y, which there usually is; hence the phrase “correlation is not causation”.1
To give an example, in order to figure out the effect of a medical treatment, you could look at differences between the people who get the treatment and the people who don’t get the treatment on various outcomes, such as the disease it’s supposed to treat, potential side-effects like mortality, and similar. The problem with this is that it is subject to reverse causality and confounding; e.g. people with the disease are probably more likely to be treated for the disease, which could make it seem like the treatment increases rather than decreases the disease. And general factors like health/age might influence the likelihood of getting the disease, and also the likelihood of negative later outcomes like death, making the naive estimate biased; this is a key concept called confounding, and it shows up everywhere.
Since there is usually some variable Z that confounds the relationship between X and Y, regression doesn’t work. Multiple regression is the naive solution to this, where one attempts to list every possible confounder Z, and include these in the statistics, with the hope that the rest of the association between X and Y is genuinely causal.
In the previous example of a medical treatment, in multiple regression one would try to measure the various confounders, like age or preexisting medical problems, to control for that.2 If you can list all of the confounders, then this solves the problem of biased estimates. If you can list some major confounders, then that might reduce the problem. But a lot of the time in practice you can’t list the confounders, or can’t measure them well enough to control for them, which makes it far from a perfect method.
If one doesn’t like assumptions, then a very popular method is experiments. In an experiment, to find out the effect of X on Y, you modify X and then observe the resulting effect on Y. The standard sort of experiment used is a randomized controlled trial, where one has two groups of individuals, one group is assigned to some intervention while another is assigned to be controls that receive no intervention. The contrast between these two groups is then taken to be an estimate of the causal effect.
This obviously requires some intervention that influences X, and doesn’t influence any things other than X. In medicine, this seems straightforward enough, because often X already is some medical intervention that needs to be tested. But even in medicine you run into the fact that some people are going to leave the treatment or similar; and both inside and outside of medicine, you run into the problem that what you often want to test isn’t an intervention per se. As part of basic research, you might be interested in the direct causal effects of variables that you don’t know how to intervene on. In such cases you might be able to intervene very indirectly, and possibly shift X too; but higher degrees of indirection leaves more space for confounding, where a “heavy-handed” intervention has influence on other things than just X.
Other methods for causal inference
People often associate causality with change over time. If you see the variable X change first, and then the variable Y change, you might start to suspect that X influences Y. This is the intuition behind Granger causality, RI-CLPM, and other similar methods. I lump them together under the label of longitudinal/time-series methods (though that is a bit simplified as there are other kinds of longitudinal methods that don’t involve this premise). These methods look at whether a change in X predicts a later change in Y, and if they do, they assume that the correlation is causal.
It’s in principle pretty simple to consider how it might be used. Suppose you want to know how, say, personality and politics are related. Then with these methods you try to measure personality and political orientation repeatedly over time, and use various clever statistical models to see if changes in one are related to changes in the other.
These methods in a way combine two different reasons that they might work. First, if X comes before Y, then it would seem that Y couldn’t influence X, ruling out reverse causality. But to me, this argument is kind of weak; reverse causality isn’t usually as big a problem as some other variable influencing both X and Y. Granger causality does to an extent address this too, though, in that if it is discovered to hold, then a common cause must be sufficiently “close” or “late” in the causal network so as to be able to match the pattern that arises in the associations over time; “shocks” to X have to predict shocks to Y.
Another powerful-sounding method for causal inference is the co-twin control method, or as Turkheimer and Harden renamed it, quasicausality. It is based on the observation that, in social science, a great deal of proposed confounds are genetic or due to nurture, so if we look at identical twins, we can control for all of these confounds. If these identical twins are discordant for X, then this provides a natural experiment that you can use to guess the effect of X on Y. Turkheimer and Harden give the example of religion and delinquency, where they find no effect after using co-twin controls.
A method that seems more popular in economics is instrumental variables. Here, you have some variable Z which forms a “natural experiment” for X. That is, if Z influences X, and is not confounded with and does not have a direct influence on Y, then Z can be used to estimate the effect of X on Y.
It is often used where Z is just some randomized experiment to begin with. For instance, a popular example given is estimating the effect of military participation on wages. Military participation is positively correlated with future income, but this might be due to the characteristics of the people who volunteer; since some are conscripted to serve in the military, this serves as an instrument that can be used for comparison, and using this, military participation was found to have the opposite effect.
Z doesn’t need to be a randomly assigned experiment like this; you could use all sorts of variables that affect X for Z. The trouble is that many variables that influence X may also be confounded with or have an influence on Y, so this needs to be ruled out when using Z as an instrument. One example that is relevant to bring up for this is Mendelian randomization; here, a genetic predisposition to X is used as the instrument Z. This can be done in non-randomized ways, but it is often safer to do in randomized ways, using the fact that genes are assigned randomly from the parents due to sexual reproduction.
A unified model: Xc/Xr splits
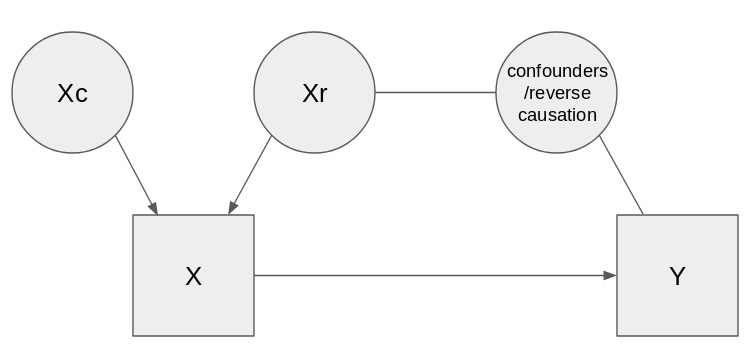
To me, what all of the previous models have in common is: You want to find the causal effect of X on Y. In order to do so, you construct a setting where X has two fragments; Xc (“X causal”) and Xr (“X residual”). Then you hope that Xc is not confounded, and regress Xc on Y to estimate the causal effect. Or more concretely:
In multiple regression, you control for some set of confounders Z. This ends up “explaining” some of the association between X and Y; this explanation you attribute to Xr. The remainder you attribute to Xc.
With randomized controlled trials, being in the experimental arm is the Xc, and any other variation is Xr.
With longitudinal/time-series methods, changes over time is Xc, while things like seasonality (predictable changes that are plausibly confounded) or individual mean differences (if studying multiple time series in parallel, e.g. time series for different people or different countries) are Xr.
With quasicausality, effects that are independent of nature and nurture are Xc, while effects that are shared between twins is Xr.
With instrumental variables, variance due to the instrument is Xc, while variance independent of the instrument is Xr.
The family of methods makes three assumptions, which are rather obvious:
Xc must be valid influence in X. This is an important point that I think there is not enough attention paid to, so we’ll come back to this in the next section.
Xc must not be confounded with Y (or similar, such as via reverse causation); its effect on Y should be solely via its effect on X. This is usually not directly testable, and one must instead have some theoretical argument for why this is so.
Xr must not be a consequence of Xc. This is a somewhat subtle technical point that I’m not going to address much here, but if you are not familiar with it, I suggest reading up on overadjustment bias.
Know your Xc!
There’s an easy way to remove all confounding from Xc; just place all of your variance in Xr, and let Xc be constant. If you want to know the effect of smoking on lung cancer, but you are worried that smokers have a gene that independently causes lung cancer, you can just control for smoking, and that gene can’t mess up your results. If Xc doesn’t vary, then it can’t be confounded. Of course, that also means that you can’t estimate the effect of X on Y; you are relying on variance in X (smoking) to estimate variance in Y (lung cancer), and controlling amounts to destroying this variance.
This is obviously a silly example, but it illustrates an important point: It is not the amount of confounding in Xc that matters, but rather the ratios of the variances in Xc. Xc should have as much unconfounded variance as possible, and as little confounded variance as possible. With multiple regression, this is often simple enough; you have a couple of confounders that you believe to be relevant, so you can adjust for those explicitly, and this likely reduces the degree of confounding because you have good reason to believe that these confounders specially problematic. You are unlikely to meaningfully reduce the valid variance much, as it would require the listed confounders to be highly predictive of X, which they rarely are. However, for many of the other methods, you often indiscriminately place huge amounts of the variance into Xr, removing it from Xc. Going back to the example of longitudinal modelling of personality and politics, a lot of personality and political orientation is stable over time; by only looking at the changes to these variables, one throws out all of this stable variance.
But do we really believe that temporary shifts in personality and politics are less confounded than long-term shifts? Remember, this is a necessary condition for these methods to work. I have no idea how to answer that question in the abstract, because I don’t know which factors influence personality and politics. The main options I could think of would be something like, changes in social environment or decisions to change one’s identity - but neither of those seem unconfounded.
And even that might be overly generous, as it assumes that things are either confounded or valid. Some studies find that if you adjust for measurement error, personality has a stability of 0.99 over different years; a lot of the apparent changes in personality might just be changes in the measurement error. Thus, this gives a third sort of variance that Xc might have, which biases the effect towards zero. You get similar problems with other methods than longitudinal methods too; for instance many traits are highly genetic (e.g. intelligence), and using quasicausality to control for the genetic influence leaves you with a tiny fraction of the original variance, which functions in unclear ways.
When I read scientific studies, I often find that they run into these sorts of problems. I’ve been thinking of ways to solve it, and each time it always runs back into the issue of, know your Xc. That is, rather than coming up with some story of how you’ve placed confounders in Xr, come up with some story for how X varies in an unconfounded way, and figure out some way to place that unconfounded variance in Xc. This severely limits the usability of the method3, because it then requires a lot of understanding for how X comes to vary in the first place, which you may not know. I think there might be a few limited examples where not knowing why Xc varies still lets you infer causality, but I find that in a lot of papers when I switch from the perspective of “can I think of some confounder that they have missed?” to “do I know why Xc varies?”, their causal inference becomes a lot less convincing; it’s not obvious that Xc varies a lot in an unconfounded way.
In future blog posts, I will look into additional problems with doing Xc/Xr splits, as well as some alternative very different methods of causal inference that are applicable in a wider range of contexts than Xc/Xr splits are.
A lot of the time, “correlation is not causation” is used in reference to other problems, such as spurious correlations or even nondeterministic causality. This is misleading, IMO, since the bigger problem most of the time is common causes.
In practice, you would also restrict yourself to the people who have the disease that is getting treated in the first place. However, that is not very relevant for my point.
One could perhaps say that one could use it as a cheap sanity-check or hypothesis-screening; if you assert a causal connection between X and Y, then there better also be a correlation, even when controlling in all of these varied ways. I agree that these sorts of sanity-checks are very valuable, but they may have some problems too, due to overadjustment bias, measurement error, as well as an as-of-yet unnamed bias that I’ve come up with which I want to address in a later blog post. Still, it’s probably fair to say that under a lot of circumstances, you can use this method to disprove causal claims, but not to prove them.

What an unusual little blog you've begun! I found you from astralcodex.com from your comment "I draw the opposite conclusion that you do. Since a lot of the psychological manifestations of 'addiction"'is just normal motivational dynamics," and I'm reading your work because you really come across as extremely intelligent and very well read.
That stated, I do think you need to work on your style! I have a sense that I already know 2/3 of what you were writing in this post, and that's the only way I was able to follow half of it.
Advice: Say less in any one post. Use more concrete examples. And, motivate posts at the outset with some kind of hook. For instance, that AstralCodex post you replied to began with potato chips; it said basically that the flow state and one's experience of addiction were the same, it talked about heroin a bit, and the whole thing worked. This post of yours seems far more important and its implications strike me as extremely interesting, but I didn't know why I was reading it (except that you seem brilliant), nothing was ever contextualized enough to follow clearly, and it was far too much to digest all at once.
Good luck, Mysterious Person From The Internet, and I'll visit you again!