If everything is genetic, then nothing is genetic

Understanding the phenotypic null hypothesis

The first law of behavioral genetics states that “All human behavioural traits are heritable.” This sounds like quite a win for behavioral genetics, yet Eric Turkheimer, the man who came up with the laws of behavioral genetics, is an avid critic of heritability. How can this be?

The trouble is that people want to interpret heritability as being a measure of how “genetically coded” or “biological” a variable is. But the first law is very broad, and so it also applies to obviously nonbiological variables like “how much education has this person received?” (educational attainment).

While there can be no doubt that much of the variation in educational attainment ultimately originates in biology, the variable itself is obviously not biological; it’s socially constructed, and in our society it is based on membership in school institutions and the degrees they hand out.

The fact that a socially constructed variable can be genetic (or at least, have a heritable component) is an important fact, and once we look closer, it tells us something about both the advantages and the limitations of behavioral genetics. (The title of this post, “then nothing is genetic”, is somewhat dismissive because it is primarily aimed at informing the people who can be excessively into genetics; however, I do think that the sense in which everything is genetic is meaningful, as you will see.)

Why is educational attainment heritable?

A variable is heritable if variation in genes act as a root cause for variation in that variable. So for instance, people differ from each other in height, and most of those differences ultimately arise because people have different genes, which influence things like skeletal growth that ultimately influence height.

Simplified model of the heritability of height.

Note an important thing here: Heritability is transitive. Genes influence skeletal growth, and skeletal growth influences height, so therefore genes influence height, and therefore height is heritable. As a general rule, there will be several intermediate variables that genes pass through before they influence a variable of interest. This is because the direct effects of genes are very simple, coding for proteins, and most traits that we are interested in are much more complex than just proteins.

This sets the stage for educational attainment. Why is educational attainment heritable? Because it is influenced by heritable traits like intelligence.¹² Note that this is not some sort of fancy “genetic causation” that differs from ordinary causation - it’s run of the mill factors like smarter people having more to gain from education, doing better on exams, etc.

Rough model of the heritability of education - there is much we don’t know, as well as much that I am not going into in this post.

This pattern generalizes. You’ve got very many variables that are connected to each other in a complex causal network. Some of these variables are “directly genetic” - but that doesn’t matter for heritability, since the directly genetic variables will causally influence the other variables, and “transfer” their heritability to them.

The phenotypic null hypothesis

We now come to the meat of the post, the phenotypic null hypothesis. When some people hear that a variable is heritable, they want to study it using genetic methods. And that can be perfectly reasonable, if done correctly.

However, often people are interested in (phenotypic) causation - that is, the effect on one variable on another variable, e.g. the effects of education on intelligence. And then at times people treat heritability as an alternative theory to variables influencing each other directly. And since variables influencing each other is the main factor that makes things heritable, “the variables are heritable” and “the variables are phenotypically influenced by other variables” are not competitive theories, but instead closely correlated with each other.

People might read that intelligence is genetically correlated with myopia, or that homosexuality is genetically correlated with depression, and conclude that these are due to a direct biological link, rather than due to smarter people straining their eyes reading or staying indoors more, or homosexual people being discriminated against. Yet as we saw with education, this assumption is unwarranted; phenotypic causality leads to heritability. That’s not to say that phenotypic causation theories are always right, or that behavioral genetic methods can’t say anything about them (we will soon see what behavioral genetics can say). Rather, it just implies that the existence of heritability is of no evidentiary value for ruling out phenotypic causality.

Put simply, the phenotypic null hypothesis is this: Heritability tells you that if you go up through the chain of causation, then you will often end up with genes. However, there may be many ways that variables can be connected to each other, and there’s no particular reason to expect that every step along the chain of causation from genes to outcomes is best thought of as biological.

The environment to the rescue

One popular solution to the phenotypic null hypothesis is to investigate phenotypic causation using “discordant twin” designs. So for instance, you might want to investigate the effect of education on income. Here you can’t just use the raw correlation between education and income, because it might be that preexisting intelligence influences both education and separately also income. To solve this, you might look at identical twins who got different amounts of education.

(Another methodology is to look at what behavioral geneticists call “environmental correlations” or “E correlations”. Discordant twins and environmental correlations are actually equivalent, but discordant twins may be easier to understand.)

Identical twins who get different amounts of education cannot have done so due to genetic factors, since their genes are identical. Meanwhile, factors like luck, e.g. being just barely on the right side of an exam score cutoff, remain just as strong. Thus, discordant twin designs hope that they can treat the discordance between the twins as basically random, which if true would make it as good as an experimental intervention.

If there is a phenotypic causal effect where education increases income, then you would expect the correlation to also appear in discordant twins, because it doesn’t matter why the twins differ in education, the differences in education should still lead to differences in income.

… or not

Suppose you want to study whether spanking as a child leads to antisocial behavior as an adult. But the trouble is, maybe some children are genetically more prone to being naughty than others, and these genes also lead to antisocial behavior in adulthood. This could bias your estimates if you just look at the correlation between the two.

So you might decide to use the discordant-twin methodology described before. Find a bunch of twin pairs, ask them how much they were spanked, and look at the ones who were spanked to different degrees. If spanking still correlates with antisocial behavior, then probably spanking causes antisocial behavior… right?

No. The first issue is that genetically identical twins are not actually fully behaviorally identical; perhaps it's due to random brain wiring, perhaps it's due to prior environmental factors, but it means there’s still going to be some variation in naughtiness left.

But perhaps a bigger issue is measurement error. You can’t really accurately know how much someone got spanked by asking them; language is vague, memory is fickle. Arguably this doesn’t break standard social science methodology because you’d still expect some signal to get through. You can get a rough picture of how much they were spanked. However, by looking at identical twins, you are controlling both for genetics and parenting styles; presumably this removes most of the genuine variance in spanking. But most of the noise stays, so the signal:noise ratio gets much, much worse.

This is a problem because a low signal:noise ratio biases the effects, often towards zero. If the twins you think are discordant actually got spanked the same amount, and just communicated the spanking differently to you, then you wouldn’t necessarily expect them to have different antisocial behavior, and even if they did, you wouldn’t necessarily expect this to be indicative of the effects of antisocial behavior.

Further, there’s a fundamental difference between genes and many environmental factors, in that genes stay with you for you entire life, having lots of time to influence you, while many environmental factors are transient. This gives genetic factors a much longer time to take effect. This too will bias discordant twin studies against identifying cases where phenotypic variables directly influence each other.

A simulation

Finally, if you are familiar with the methods used in behavioral genetics, but not familiar with the notion of the phenotypic null hypothesis, it may be helpful for me to do a simulation. Suppose we have data generated according to the following mechanism:

Two variables (nodes X and Y) that are predominantly genetic (A), though with a bit of nonshared environmental influence (E), and a tiny smidge of family nurture influence (C), which are causally related to each other (X → Y) and measured with “barely-acceptable” reliability (X → Xobs, Y → Yobs).

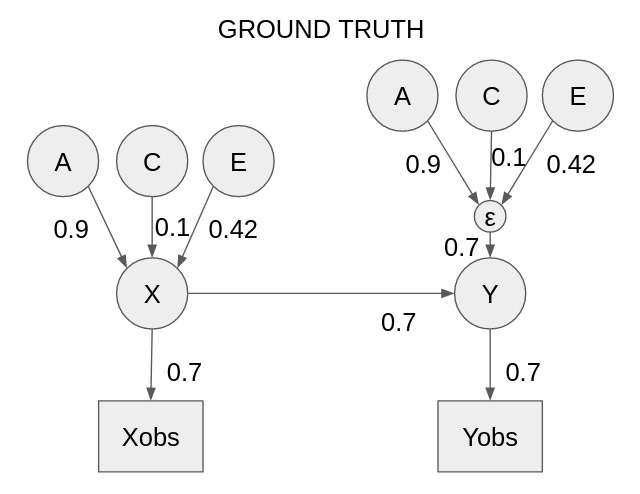
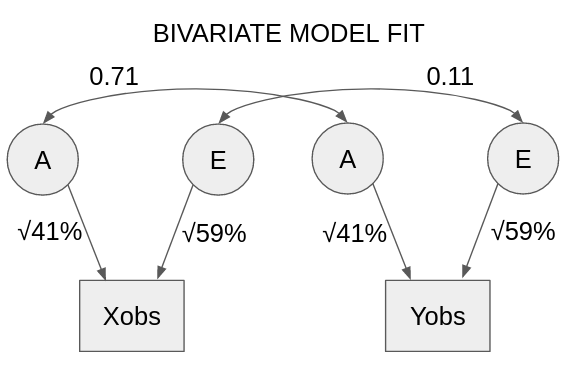
In this case, we could try to fit a bivariate behavioral genetic model to it. Using the standard behavioral genetic reporting methods, it would end up looking like this:

Bivariate AE model, finding strong genetic correlation and weak environmental correlation.

There’s a lot going on here, so unless you are strong in structural equation modelling, I wouldn’t necessarily expect you to follow it all.³ The main thing to note for the purposes of this post is that the genetic correlation has ended up much bigger than the environmental correlation. This happened due to the measurement error; if it was not for the measurement error, they would be of similar magnitudes.

Thanks to Justis Mills for proofreading and feedback. This post can also be found on LessWrong.

Code for the simulation can be found here:

import numpy as np

N = 1000000

def gen_var(zygozity, a, c, e):
    if zygozity == "MZ":
        A = np.random.normal(0, 1, N)
        C = np.random.normal(0, 1, N)
        E = np.random.normal(0, 1, (2, N))
        return a * A + c * C + e * E
    elif zygozity == "DZ":
        A = np.random.normal(0, 1, (2, N))
        A[0, :] = 0.5 * A[1, :] + np.sqrt(1-0.5**2) * A[0, :] # rDZ = 0.5
        print(np.cov(A))
        C = np.random.normal(0, 1, N)
        E = np.random.normal(0, 1, (2, N))
        return a * A + c * C + e * E

def measurement_error(x):
    return 0.7 * x + np.random.normal(0, 0.7, (2, N))

def sim(zygozity):
    x = gen_var(zygozity, 0.9, 0.1, 0.42)
    y = 0.7 * x + 0.7 * gen_var(zygozity, 0.9, 0.1, 0.42)
    return measurement_error(x), measurement_error(y)

def ace(rMZ, rDZ, rself=1.0):
    a2 = 2 * (rMZ - rDZ)
    c2 = rDZ - 0.5 * a2
    e2 = rself - a2 - c2
    return a2, c2, e2

def ace_uni(vMZ, vDZ):
    rMZ = np.corrcoef(vMZ)[0, 1]
    rDZ = np.corrcoef(vDZ)[0, 1]
    return np.sqrt(ace(rMZ, rDZ)) # https://openpsych.net/paper/61/

def ace_bivar(xMZ, xDZ, yMZ, yDZ):
    ax, cx, ex = ace_uni(xMZ, xDZ)
    ay, cy, ey = ace_uni(yMZ, yDZ)
    XYr =  np.corrcoef(np.concatenate([xMZ[0], xMZ[1], xDZ[0], xDZ[1]]), np.concatenate([yMZ[0], yMZ[1], yDZ[0], yDZ[1]]))[0, 1]
    XYrMZ = np.mean([np.corrcoef(xMZ[0, :], yMZ[1, :])[0, 1], np.corrcoef(xMZ[1, :], yMZ[0, :])[0, 1]])
    XYrDZ = np.mean([np.corrcoef(xDZ[0, :], yDZ[1, :])[0, 1], np.corrcoef(xDZ[1, :], yDZ[0, :])[0, 1]])
    axy, cxy, exy = ace(XYrMZ, XYrDZ, XYr)
    return axy / (ax * ay), cxy / (cx * cy), exy / (ex * ey)

xMZ, yMZ = sim("MZ")
xDZ, yDZ = sim("DZ")

print(ace_uni(xMZ, xDZ)) # => a = 0.64ish, c = 0.08ish, e=0.77ish
# or if you prefer in quadratic terms, a2 = 0.40ish, c2 = 0.01ish, 0.59ish
# print(ace_uni(yMZ, yDZ)) # <- no need for this since it gives the same results as with x

print(ace_bivar(xMZ, xDZ, yMZ, yDZ)) # => rA = 0.7ish, rE = 0.11ish, rC = all over the place

1. Of course, education is also influenced by environmental factors too. Twin studies tend to find education to be one of the more environmentally influenced traits. However, the specific details are still getting worked out, and there are reasons to believe that the environment is both overestimated and underestimated.

2. Why is intelligence heritable? Dunno, that’s still an open research question.

3. Some things not mentioned in the main article: Twin studies often don’t model measurement error correctly, which means that even though the traits were almost entirely genetically determined, the model actually claimed it to be about 50-50 genes vs environment. Furthermore, twin studies cannot detect effects that are close to 0, so the nurture (C) component had to go. And twin studies usually present the genetic and environmental influences in a squared, rather than linear way.