[LDSL#0] Some epistemological conundrums

This post is also available on LessWrong.

When you deal with statistical science, causal inference, measurement, philosophy, rationalism, discourse, and similar, there’s some different questions that pop up, and I think I’ve discovered that there’s a shared answer behind a lot of the questions that I have been thinking about. In this post, I will briefly present the questions, and then in a followup post I will try to give my answer for them.

Why are people so insistent about outliers?

A common statistical method is to assume an outcome is due to a mixture of observed factors and unobserved factors, and then model how much of an effect the observed factors have, and attribute all remaining variation to unobserved factors. And then one makes claims about the effects of the observed factors.

But some people then pick an outlier and demand an explanation for that outlier, rather than just accepting the general statistical finding:

In fact, aren’t outliers almost by definition anti-informative? No model is perfect, so there’s always going to be cases we can’t model. By insisting on explaining all those rare cases, we’re basically throwing away the signal we can model.

A similar point applies to reading the news. Almost by definition, the news is about uncommon stuff like terrorist attacks, rather than common stuff like heart disease. Doesn’t reading such things invert your perception, such that you end up focusing on exactly the least relevant things?

Why isn’t factor analysis considered the main research tool?

Typically if you have a ton of variables, you can perform a factor analysis which identifies a set of variables which explain a huge chunk of variation across those variables. If you are used to performing factor analysis, this feels like a great way to get an overview over the subject matter. After all, what could be better than knowing the main dimensions of variation?

Yet a lot of people think of factor analysis as being superficial and uninformative. Often people insist that it only yields aggregates rather than causes, and while that might seem plausible at first, once you dig into it enough, you will see that usually the factors identified are actually causal, so that can’t be the real problem.

A related question is why people tend to talk in funky discrete ways when careful quantitative analysis generally finds everything to be continuous. Why do people want clusters more than they want factors? Especially since cluster models tend to be more fiddly and less robust.

Why do people want “the” cause?

There’s a big gap between how people intuitively view causal inference (often searching for “the” cause of something), versus how statistics views causal inference. The main frameworks for causal inference in statistics are Rubin’s Potential Outcomes framework and Pearl’s DAG approach, and both of these view causality as a function from inputs to outputs. In these frameworks, causality is about functional input/output relationships, and there are many different notions of causal effects, not simply one canonical “cause” of something.

Why are people dissatisfied with GWAS?

In genome-wide association searches, researchers use statistics to identify alleles that are associated with specific outcomes of interest (e.g. health, psychological characteristics, SES outcomes). They’ve been making consistent progress over time, finding tons of different genetic associations and gradually becoming able to explain more and more variance between people.

Yet GWAS is heavily criticized as “not causal”. While there are certain biases that can occur, those biases are usually found to be much smaller than seems justified by these critiques. So what gives?

What value does qualitative research provide?

Qualitative research makes use of human intuition and observation rather than mathematical models and rigid measurements. But surely ultimately human cognition grounds out to some algorithms that could be formalized. Maybe it’s just a question of humans having more prior information and doing more comprehensive observation? But in that case, it seems like sufficiently intensive quantitative methods should outperform qualitative research, e.g. if you measure everything and throw it into some sort of AI-based autoregressive model. Right?

Yet this hasn’t worked out well so far. Is it just because we are not trying hard enough? For instance obviously human sight has much higher bandwidth than questionnaires, so maybe questionnaires would miss most of the information and we need some video surveillance thing with automatic AI tagging for it to work properly.

Or is there some more fundamental difference between qualitative research and quantitative research?

What’s the distinction between personality disorders and “normal” personality variation?

Personality disorders resemble normal personality variation. Self-report scales meant to measure one often turn out to be basically identical to self-report scales meant to measure the other. This leads a lot of people to propose that personality disorders are just the extreme end of personality variation, but is that really true? If not, why not?

What’s more, sometimes mental disorders really seem like they should be the extreme end of normal personality, but aren’t. For instance, Obsessive-Compulsive Disorder seems conceptually similar to Conscientious personality (in the Big 5 model), but results on whether they are connected are at best mixed and more realistically find that OCD is something different from Conscientiousness. Similarly, Narcissism is often described similarly to Disagreeable-tinted Extraversion, but it doesn’t appear to be the same.

What is autism?

Autism is characterized by a combination of neurological symptoms and poor social skills. Certainly one of the strongest indicators of autism is that both autistic and non-autistic people tend to agree that autistic people have poor social skills, but quantitative psychologists often struggle with operationalizing social skills, and in my own brief research on the topic, I haven’t found a clear difference in social performance between autistic and non-autistic people. What’s going on?

Some propose a double empathy problem, where autistic people aren’t necessarily socially broken, but rather have a different focus than non-autistic people. That may be true, but then what is that focus?

Some propose an empathizing/systemizing tradeoff, where male and autistic brains are better able to deal with predictable systems, whereas female and allistic brains are better able to deal with people. Yet this seems to mix together technical interests with autistic interests, and mix together antisocial behavior with social confusion.

Also, why do some things, like excessively academic ideas that haven’t been tested in practice, seem similar to autism? Am I just confused, or is there something going on there?

What is gifted child syndrome/twice-exceptionals?

There’s this idea that autism, ADHD, and high IQ go together in a special way. That said, it’s not really borne out well statistically (autism and ADHD are if anything negatively correlated with IQ), and so presumably it’s just an artifact, right?

What’s up with psychoanalysts?

Psychoanalysts have bizarre-to-me models, where it often seems like they treat people as extremely sensitive, prone to spinning out crazily after even quite mild environmental perturbations.

When statistical evidence contradicts these views, they typically dismiss this by saying that the measurement is wrong because it lacks nuance, or because people lack self-awareness.

Yet to me that just raises the question of why they would conclude this in the first place.

Why are some ideas more “robust” than others?

Some ideas seem “ungrounded”; informally, they are many layers of speculation removed from observations, and can turn out to be false and therefore worthless. Meanwhile, other ideas seem strongly “grounded”. Newtonian physics, even if it is literally false (as we have measured to high precision, relativity is more accurate) and ontologically confused (there isn’t some global flat space with masses that have definite positions and velocities), is still extremely useful.

One solution is to say that Newtonian physics is an approximation to the truth and that makes it quite useful. There’s some value to this answer, but it seems to suggest that the mere fact of being an approximation is sufficient to make something grounded, which doesn’t seem borne out in practice.

How can probability theory model bag-like dynamics?

Probability theory has an easy time modelling very rigid dynamics, where you have a fixed set of variables that are related in a simple way, e.g. according to a fixed DAG.

However, intuitively, we often think of systems that are much more dynamic. For instance, in physical systems, we often model there as being a set of objects. These objects don’t have a fixed DAG of interactions, as e.g. collisions depend on the positions of the objects. You end up with situation where the structure of the system depends on the state of the system, which is feasible enough to handle in e.g. discrete simulations, but hard to get a clean mathematical description of.

Why would progressivism have paradoxical effects on diversity?

Some anti-woke discourse argues that anti-stereotyping norms undermine diversity by preventing people from developing models of minorities’ interests. But isn’t there so much variation within demographic groups that you pretty much have to develop individual models anyway? Furthermore, isn’t there usually a knock-on thing where something that is a common problem among a minority is also a sometimes-occurring problem among the majority, such that you can use shared models anyway?

If there is diversity that needs to be taken into account, wouldn’t something statistical that directly focuses on the factors we care about, rather than on demographics, be more effective?

Why don’t people care about local validity and coherence?

It seems like local validity is a key to sanity and civilization - this sort of forms the basis for rationalism as opposition to irrationalism. Yet some people resist this strongly - why? I think there’s often a lack of trust underlying it, but why?

Relatedly, some people hold a dialectic style of argument to be superior, where a thesis must be contrasted with a contradictory counter-thesis, and a resolution that contains both must be found. They sometimes dismiss their counterparties as “eristic” (i.e. rationalizing reasons for denial), even when those counterparties just genuinely disagree. Yet isn’t “I haven’t seen convincing reason to believe this” a valid position?

How does commonsense reasoning avoid the principle of explosion?

In logic, the principle of explosion asserts that a single contradiction invalidates the entire logic because it allows you to deduce everything and thus makes the logic trivial. Yet people often seem to navigate through the world while having internal contradictions in their models - why?

What’s wrong with symptom treatment?

I mean, obviously if you can more cheaply cure the root cause than you can mitigate the harm of some condition by reducing the symptoms, you should do that. But this seems like a practical/utilitarian consideration, whereas some people treat symptom treatment as obviously-bad and almost “dirty”.

Why does medicine have such funky qualitative reasoning?

Rather than making up a pros and cons list, when reading about medical theory I often hear about “indications” and “contraindications”, where a contraindication is not treated as a downside, but rather as invalidating an entire line of treatment.

Also, there’s things like blood tests where people are classified binarily on whether they are “outliers”, despite there being substantial natural variation from person to person.

What does it mean to explain a judgement?

If you e.g. use AI to predict outcomes, you get a function that judges datapoints by their likely outcomes. But just the judgement on its own can feel too opaque, so you often want some explanation of why that was the judgement it gave.

There’s a lot of ideas for this, e.g. the simplest is to just give the weights of the function so one can see how it views different datapoints. This is often dismissed as being too complex or uninterpretable, but what would a better, more interpretable method look like? Presumably sometimes there just is no better method, if the model is intrinsically complex?

Why do people seem to be afraid of measuring things?

There’s lots of simple statistical models which make measurement using proxy data super easy. Why aren’t they used more? In fact, why do people seem to be afraid of using it, complaining about biases, often going out of their way to hide information relevant to developing these measurements?

Obviously no measurement is perfect, but it seems like the solution to bad measurement is more measurement, right?

Why is there no greater consensus for large-scale models?

We all know outcomes depend on multiple causes, to the point where things can be pretty intertwined. In genomics, people are making progress on this by creating giant models that take the whole genome into account. Furthermore I’ve had a long period where I was excited about things like Genomic SEM, which also start taking multiple outcome variables into account, modelling how they are linked to each other.

As Scott Alexander argued in the omnigenic model as the metaphor for life, shouldn’t this be how all of science works? Isn’t much of science deeply flawed because it doesn’t put enough effort into scale?

Can we “rescue” the notion of objectivity?

It seems obvious that there’s a distinction between lying and factual reporting, but you can create a misleading picture while staying entirely factual via selective reporting: only report the facts which support the picture you want to paint, and avoid mentioning the facts that contradict it. This seems “wrong” and “biased”, but ultimately there are a lot of facts, so you have to be selective; and it seems like the selectiveness should be unrepresentative to emphasize blessed over barren or cursed information.

What lessons can we even learn from long-tailedness?

Some people point out that certain statistical models are flawed because they assume short-tailed variables when really reality is long-tailed, calling it the “ludic fallacy”. OK, that seems like an obviously valid complaint, so basically you should adjust the models to use long tails, right? But that often leads to further complaints about the “ludic fallacy”, Knightian uncertainty, and that one is missing the point.

But isn’t the entire point of long-tailedness that rare crazy unpredictable factors can pop up? If not, what is the point of talking about long-tailedness?

Perception is logaritmic; doesn’t this by default solve a lot of problems?

In a lot of ways, perception is logarithmic; for instance even though both columns in the picture below add 10 dots, you perceive the left one as having a much bigger difference than the right one:

Logaritmic perception is quite useful because it allows one to use the same format to store quantities across orders of magnitude. It’s arguably also typically used in computers (floating point) and science (scientific notation). In psychophysics, this is known as the Weber-Fechner law, that perception (S) is logarithmically related to intensity (I).

While logarithmic perception is just a fact, wouldn’t this fact often make long-tailedness a non-issue, because it means certain measurements (e.g. psychological self-reports) are implicitly logarithmic, and so the statistical models on them implicitly have lognormal residuals?

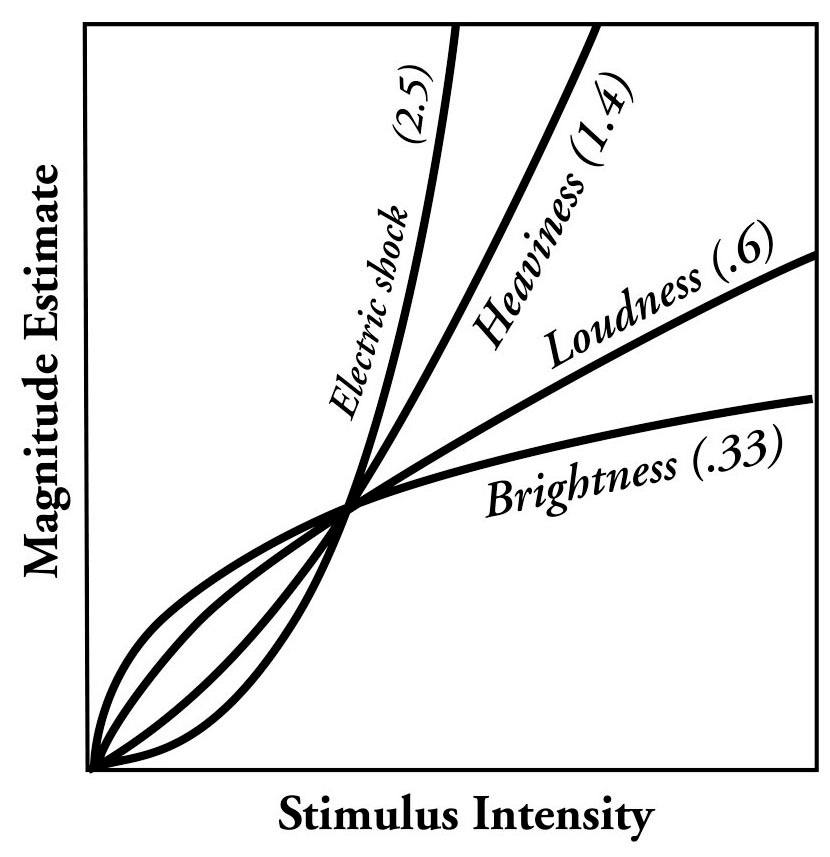
Also, sometimes (e.g. for electric shocks or heaviness) perception is not logarithmic, but instead superlinear. Steven’s power law models it as, well, a power law:

It seems quite sensible why that would be the case: sometimes things matter superlinearly, e.g. there’s a limit to how heavy things you can lift, so of course the weight perception is gonna rapidly accelerate close to that limit. But this just seems to mean that human perception is nicely calibrated to emphasize how important things are, which just means we are generally blessed to not have to worry that much about perception calibration, right?

This seems related to how in psychometrics, there’s a lot of fancy models for quantitatively scoring tests (e.g. item response theory), but they tend to yield results that are 0.99 correlated with basic methods like adding up the items, so they aren’t all that important unless you’re doing something subtle (e.g. testing for bias).

More generally, in order to measure or perceive some variable X, it’s necessary for X to influence the measurement instrument. The standard measurement model is to just say that the measurement result is X + random noise. If (simplifying a bit) you add up the evidence that X has influenced the measurement device, that seems like the most direct measurement of X you could imagine, and it also pretty much gets you some number that has maximal mutual information with X. Doesn’t that seem like a pretty reasonable way of measuring things? So measurement is by-default correct.

All of this may be wrong

I posed a lot of conundrums, and gave some reasons why one might dismiss those conundrums, and essentially dismiss people acting in these ways as irationally overgeneralizing from a few edge-cases where it does make sense. This is essentially scientism, the position that human thinking has lots of natural defects that should be fixed by understanding universally correct reasoning heuristics.

However, under my current model, which I will explain in my next posts, it’s instead the opposite that is the case: that universally correct reasoning heuristics have lots of defects that can be fixed by engagement with nature.

I’m not sure my model will explain all of the above problems. Possibly some of my explanations are basically just hallucinatory. But these are at least useful as examples of the sorts of things I expect it to explain.

Continued in: Performance optimization as a metaphor for life.